Answer:
No, the sum of all the probabilities is not equal to 1.
Explanation:
Given
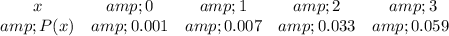
Required
Determine if the given parameter is a probability distribution
For a probability distribution to exist, the following must be true;
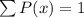
So, we have:
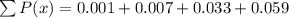
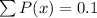
Hence, it is not a probability distribution because the sum of all probabilities is not 1