Question

Find the dimensions of a rectangle with area 3 square meters whose perimeter is as small as possible.

Answer 1

The perimeter is minimum for Length and width both are
`\sqrt3`.

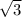Explanation:

Area, A = 3 square metre

Let the length is L and width is W.

Area = L W

3 = L W.....(1)

The perimeter is given by

P = 2 (L + W)

Substitute the value of from (1)

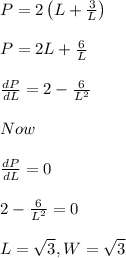
`P = 2 \left ( L +(3)/(L) \right )\\\\P = 2 L + (6)/(L)\\\\(dP)/(dL) = 2 - (6)/(L^2)\\\\Now\\\\(dP)/(dL)=0\\\\2 - (6)/(L^2) = 0\\\\L = \sqrt 3, W = \sqrt 3`

Now

`(d^2P)/(dL^2)=(12)/(L^3)\\`

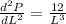
It is alays positive, so the perimeter is minimum.