Question

The function f(t) = 4t2 − 8t + 7 shows the height from the ground f(t), in meters, of a roller coaster car at different times t. Write f(t) in the vertex form a(x − h)2 + k, where a, h, and k are integers, and interpret the vertex of f(t).

Answer 1

Vertex form is f(t) = 4
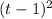`(t-1)^(2)` +3 and vertex is (1, 3).

Explanation:

It is given that f(t)= 4
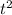`t^(2)` -8 t+7

Let's use completing square method to rewrite it in vertex form.

Subtract both sides 7

f(t)-7 = 4
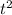`t^(2)` -8t

Factor the 4 on the right side.

f(t) -7 = 4(
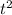`t^(2)` - 2 t)

Now, let's find the third term using formula
`((b)/(2) )^(2)`

Where 'b' is coefficient of 't' term here.

So, b=-2

Find third term using the formula,

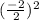`((-2)/(2) )^(2)` which is equal to 1.

So, add 1 within the parentheses. It is same as adding 4 because we have '4' outside the ( ). So, add 4 on the left side of the equation.

So, we get

f(t) -7 +4 = 4(
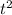`t^(2)` -2 t +1)

We can factor the right side as,

f(t) -3 = 4
`(t-1)^(2)`

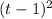
Add both sides 3.

f(t) = 4
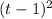`(t-1)^(2)` +3

This is the vertex form.

So, vertex is (1, 3)