Answer:
Explanation:
From the picture attached,
m∠COB = 90° - m∠BOS
= 90° - 40°
= 50°
tan(30°) =
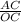
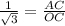
AC =
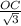 ------(1)
------(1)
Similarly, tan(50°) =
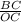
BC = OC[tan(50°)] -------(2)
Now AC + BC = 30 cm
By substituting the values of AC and BC from equation (1) and (2),
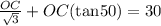
(1.769)OC = 30
OC = 16.96
1). cos(30°) =

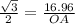
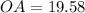 cm
cm
Therefore, distance between the ship and town A is 19.58 cm.
2). cos(50°) =

0.6428 =

OB = 26.38 cm
Therefore, distance between the ship and town B is 26.38 cm.