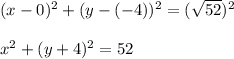Question

Find the equation of a circle with a center at (0, -4) and a point on the circle is (6, 0).

Answer 1

`x^2 + ( y + 4)^2 = 52`

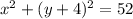
Explanation:

Equation of circle with center (a , b) and radius, r is :

`(x -a)^2 + ( y -b)^2 = r^2`

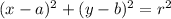
Given : a = 0 , b = - 4

Step 1 : Find the radius.

Given ( 6 , 0 ) lies on the circle. Therefore the distance between the center (0 , - 4) of the circle and ( 6 , 0 ) gives the radius of the circle.

`r = √(( 0 - 6)^2 + ( -4 - 0)^2) \\\\`

`= √( 36 + 16 ) \\\\= √(52)`

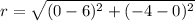
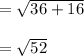
Step 2 : Equation of circle.

`(x - 0)^2 + (y -( - 4))^2 = (√(52))^2\\\\x^2 + ( y+ 4)^2 = 52`