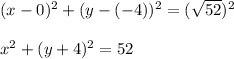Answer:
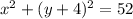
Explanation:
Equation of circle with center (a , b) and radius, r is :
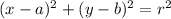
Given : a = 0 , b = - 4
Step 1 : Find the radius.
Given ( 6 , 0 ) lies on the circle. Therefore the distance between the center (0 , - 4) of the circle and ( 6 , 0 ) gives the radius of the circle.
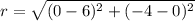
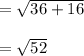
Step 2 : Equation of circle.