Question

Give FIVE (5) real life examples of functions

Answer 1

Physics - The position of a particle experimenting an uniform accelerated motion. (Quadratic function)

Chemistry - The velocity of the chemical reaction as a function of temperature. (Exponential function)

Physics - Convective heat transfer of an element with its surroundings. (Linear function)

Physics - Time conversion from seconds to minutes. (Linear function)

Physics - Radiative heat transfer from an element. (Quartic function)

Explanation:

There are many examples of applications of function in real life:

Physics - The position of a particle experimenting an uniform accelerated motion. (Quadratic function)

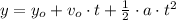`y = y_(o) + v_(o)\cdot t + (1)/(2)\cdot a \cdot t^(2)` (1)

Where:

`y` - Current position.

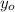`y_(o)` - Initial position.

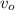`v_(o)` - Initial velocity.

`a` - Acceleration.

`t` - Time.

Chemistry - The velocity of the chemical reaction as a function of temperature. (Exponential function)

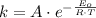`k = A\cdot e^{-(E_(o))/(R\cdot T) }` (2)

Where:

`A` - Frequency factor.

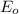`E_(o)` - Activation energy.

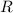`R` - Ideal gas constant.

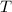`T` - Temperature.

`k` - Kinetic constant.

Physics - Convective heat transfer of an element with its surroundings. (Linear function)

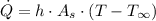`\dot Q = h\cdot A_(s) \cdot (T-T_(\infty))` (3)

Where:

`h` - Convective constant.

`A_(s)` - Surface area.

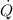`\dot Q` - Heat transfer rate.

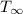`T_(\infty)` - Temperature of the surroundings.

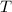`T` - Surface temperature of the element.

Physics - Time conversion from seconds to minutes. (Linear function)

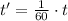`t' = (1)/(60)\cdot t` (4)

Where:

`t` - Time, in seconds.

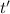`t'` - Time, in minutes.

Physics - Radiative heat transfer from an element. (Quartic function)

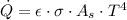`\dot Q = \epsilon \cdot \sigma \cdot A_(s)\cdot T^(4)` (5)

Where:

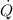`\dot Q` - Heat transfer rate.

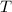`T` - Surface temperature of the element.

`A_(s)` - Surface area.

`\epsilon` - Emissivity.

`\sigma` - Stefan-Boltzmann constant.