Answer:
The volume is increasing at a rate of 25,133 mm/s.
Explanation:
Diameter is 40mm
Radius is half the diameter, so
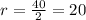
How fast is the volume increasing when the diameter is 40mm?
We have to apply implicit differentiation, of V and r in function of t. So
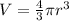
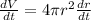
The radius of a sphere is increasing at a rate of 5 mm/s.
This means that
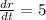
Then
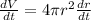
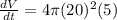
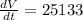
The volume is increasing at a rate of 25,133 mm/s.