Answer:
3.464 seconds.
Step-by-step explanation:
We know that we can write the period (the time for a complete swing) of a pendulum as:
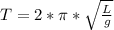
Where:
L is the length of the pendulum
g is the gravitational acceleration:
g = 9.8m/s^2
We know that the original period is of 2.00 s, then:
T = 2.00s
We can solve that for L, the original length:
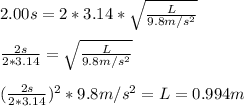
So if we triple the length of the pendulum, we will have:
L' = 3*0.994m = 2.982m
The new period will be:
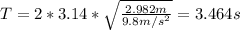
The new period will be 3.464 seconds.