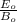Answer:
a) He found the same value of q/m for different cathode materials.
b) y =
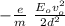 , c) v =
, c) v =
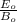
Step-by-step explanation:
In Thomson's experiments he was able to measure the deflection of the light beam under the effect of the magnetic field and with these results find the e / m relationship, which in all cases is the same, therefore the most important conclusion is that the value e E / m is constant for all materials.
b) In the part of the plates the electrons are accelerated by the electric field,
F = ma
- e E = m a
a = - (e/m) E₀
the distance traveled is
X axis
x = v₀ t
the separation of the plates is x = d
t = vo / d
Y axis
y = v_{oy} t + ½ to t²
y = ½ a t²
y =
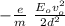
c) In this case there is a magnetic field B₀ and the electrons have no deflection
F = - e E + e v x B
if there is no deviation F = 0
e E = e v B
v =