Answer:
(a)

Explanation:
We are given that
Half life of radium-226=1620 yr
The quantity left Q(t) after t years is given by

a. We have to convert the given function into an exponential function using base e.

=
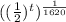
=
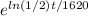
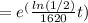
=

(b)
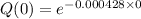
=1
From original function
Q(0)=1
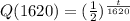
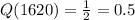
From exponential function

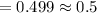
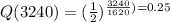

Q(3240)=0.249=
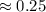
Hence, verified.