We know that:
Since line m is parallel to line n, (6x - 5) and (6x + 5) are a linear pair.
Linear pair means that the sum of two angles equaling 180°.
This means that:
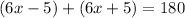
Step-by step calculations:
Opening the parenthesis:
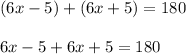
Combining like terms:
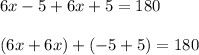
Simplify the LHS:
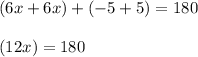
Divide 12 both sides and simplify:
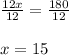
Thus, the value of x is 15.