Answer:
We arrange one of the 2μF capacitors in parallel to the other two capacitors which will be arranged in series
Step-by-step explanation:
The number of capacitors in the network = 3
The capacitance of the each capacitor, C₁, C₂, and C₃ = 2 μF
The sum of capacitors in series = The inverse of the sum of the reciprocals of the capacitances of the capacitor
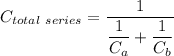
The sum of capacitances of capacitors arranged in parallel = The sum of the individual capacitances in parallel
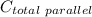 = Cₐ + C
= Cₐ + C

By placing two of the capacitors in series, and the third in parallel to the first two, we get;
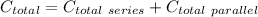

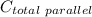 =
=
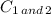 + C₃
+ C₃
∴
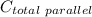 = 1 μF + 2μF= 3 μF
= 1 μF + 2μF= 3 μF
Therefore, to get a capacitor of capacity of 3 μF from 3 capacitors of
2 μF, one of the capacitors is arranged in parallel across the other two capacitors arranged in series.