Answer:
T = 1,096 10⁵ s
Step-by-step explanation:
For this exercise we can use Kepler's third law which is an application of Newton's second law
F = ma
force is gravitational force
F = G m M / r²
centripetal acceleration
a = v² / r
we substitute
G M / r² = v² / r
v² = GM / r
since the orbit is circular, we can use the uniform motion kinematics relations
v = d / t
the distance of a circle is
d = 2π r
v = 2π r / T
in this case the time has the name e period t = T
4π² r² /T² = GM / r
T² = (4π² /GM) r³
let's use the initial data to find the value of the constant
let's reduce the magnitudes to the SI system
r₁ = 384000 km (1000 m / 1 km) = 3.84 10⁶ m
T₁ = 27 day (24 h / 1 day) (3600 s / 1h) = 2.3328 10⁶ s
we look for the constant
Ks = 4π² / GM
T₁² = Ks r₁³
Ks = T₁² / r₁³
Ks = (2.3328 10⁶ )² / (3.84 10⁶ )³
Ks = 9.61 10⁻⁸
now we can determine the period of the satellite in an orbit of
r = 500 km = 5 10⁵ m
T² = 9.61 10⁻⁸ (5 10⁵ )³
T =
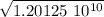
T = 1,096 10⁵ s