Question

The moon with orbital radius 384 000 km takes 27 days to complete the orbiting of the earth, determine the period of orbiting for a satellite at height 500 km from the earth surface.​

Answer 1

T = 1,096 10⁵ s

Step-by-step explanation:

For this exercise we can use Kepler's third law which is an application of Newton's second law

F = ma

force is gravitational force

F = G m M / r²

centripetal acceleration

a = v² / r

we substitute

G M / r² = v² / r

v² = GM / r

since the orbit is circular, we can use the uniform motion kinematics relations

v = d / t

the distance of a circle is

d = 2π r

v = 2π r / T

in this case the time has the name e period t = T

4π² r² /T² = GM / r

T² = (4π² /GM) r³

let's use the initial data to find the value of the constant

let's reduce the magnitudes to the SI system

r₁ = 384000 km (1000 m / 1 km) = 3.84 10⁶ m

T₁ = 27 day (24 h / 1 day) (3600 s / 1h) = 2.3328 10⁶ s

we look for the constant

Ks = 4π² / GM

T₁² = Ks r₁³

Ks = T₁² / r₁³

Ks = (2.3328 10⁶ )² / (3.84 10⁶ )³

Ks = 9.61 10⁻⁸

now we can determine the period of the satellite in an orbit of

r = 500 km = 5 10⁵ m

T² = 9.61 10⁻⁸ (5 10⁵ )³

T =
`\sqrt{ 1.20125 \ 10^(10)}`

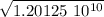
T = 1,096 10⁵ s