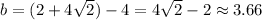Answer:
Our two numbers are:
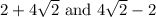
Or, approximately 7.66 and 3.66.
Explanation:
Let the two numbers be a and b.
One positive real number is four less than another. So, we can write that:
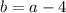
The sum of the squares of the two numbers is 72. Therefore:
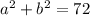
Substitute:
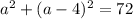
Solve for a. Expand:
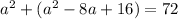
Simplify:
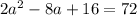
Divide both sides by two:
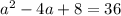
Subtract 36 from both sides:
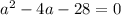
The equation isn't factorable. So, we can use the quadratic formula:
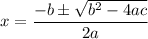
In this case, a = 1, b = -4, and c = -28. Substitute:
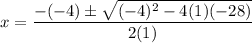
Evaluate:
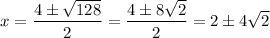
So, our two solutions are:

Since the two numbers are positive, we can ignore the second solution.
So, our first number is:
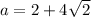
And since the second number is four less, our second number is: