Answer:

Explanation:
We are given that:

Recall that cosine is the ratio of the adjacent side to the hypotenuse. Using the Pythagorean Theorem, solve for the opposite side (we can ignore the negative for now):
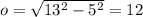
And since θ is in QII, sine is positive, and cosine and tangent are both negative.
Sine is the ratio of the opposite side to the hypotenuse. Therefore:
