Answer:
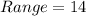
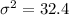
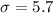
The standard deviation will remain unchanged.
Explanation:
Given
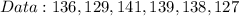
Solving (a): The range
This is calculated as:
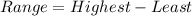
Where:
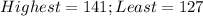
So:
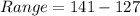
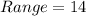
Solving (b): The variance
First, we calculate the mean
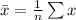
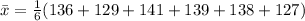
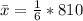
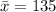
The variance is calculated as:
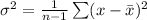
So, we have:
![\sigma^2 =(1)/(6-1)*[(136 - 135)^2 +(129 - 135)^2 +(141 - 135)^2 +(139 - 135)^2 +(138 - 135)^2 +(127 - 135)^2]](https://img.qammunity.org/2022/formulas/mathematics/high-school/pc20r1gyxxm5qup2ya4esjm5r0oy63jqtg.png)
![\sigma^2 =(1)/(5)*[162]](https://img.qammunity.org/2022/formulas/mathematics/high-school/nml0fopotirruahrjr2oedo2zw0qeid4qs.png)
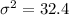
Solving (c): The standard deviation
This is calculated as:
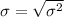
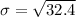
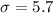 --- approximately
--- approximately
Solving (d): With the stated condition, the standard deviation will remain unchanged.