Question

Six different​ second-year medical students at Bellevue Hospital measured the blood pressure of the same person. The systolic readings​ (in mmHg) are listed below. Find the​ range, variance, and standard deviation for the given sample data. If the​ subject's blood pressure remains constant and the medical students correctly apply the same measurement​ technique, what should be the value of the standard​ deviation?

Answer 1

`Range=14`

`\sigma^2 =32.4`

`\sigma = 5 .7`

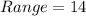
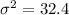
The standard deviation will remain unchanged.

Explanation:

Given

`Data: 136, 129, 141, 139, 138, 127`

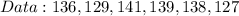
Solving (a): The range

This is calculated as:

`Range = Highest - Least`

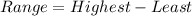
Where:

`Highest = 141; Least = 127`

So:

`Range=141-127`

`Range=14`

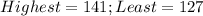
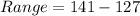
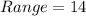
Solving (b): The variance

First, we calculate the mean

`\bar x = (1)/(n) \sum x`

`\bar x = (1)/(6) (136+ 129+ 141+ 139+ 138+ 127)`

`\bar x = (1)/(6) *810`

`\bar x = 135`

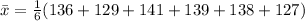
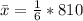
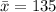
The variance is calculated as:

`\sigma^2 =(1)/(n-1)\sum(x - \bar x)^2`

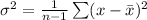
So, we have:

`\sigma^2 =(1)/(6-1)*[(136 - 135)^2 +(129 - 135)^2 +(141 - 135)^2 +(139 - 135)^2 +(138 - 135)^2 +(127 - 135)^2]`

`\sigma^2 =(1)/(5)*[162]`

`\sigma^2 =32.4`

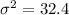
Solving (c): The standard deviation

This is calculated as:

`\sigma = \sqrt {\sigma^2 }`

`\sigma = \sqrt {32.4}`

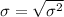
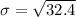
`\sigma = 5 .7` --- approximately

Solving (d): With the stated condition, the standard deviation will remain unchanged.