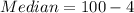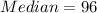Question

2071 Old Q.No.5 Person's coefficient of skewness for a distribution is 0.4 and its coefficient of variation is 30%. If mode is 88, find mean and median.​

Answer 1

`Mean = 100`

`Median = 96`

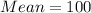
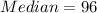
Explanation:

Given

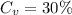`C_v = 30\%` --- coefficient of variation

`mode = 88`

`Skp = 0.4`

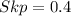
Required

The mean and the median

The coefficient of variation is calculated using:

`C_v = (\sigma)/(\mu)`

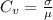
Where:

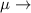`\mu \to` mean

So:

`30\% = (\sigma)/(\mu)`

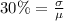
Express percentage as decimal

`0.30 = (\sigma)/(\mu)`

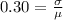
Make
`\sigma` the subject

`\sigma = 0.30\mu`

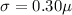
The coefficient of skewness is calculated using:

`Skp = (\mu - Mode)/(\sigma)`

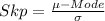
This gives:

`0.4 = (\mu - 88)/(\sigma)`

Make
`\sigma` the subject

`\sigma = (\mu - 88)/(0.4 )`

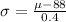
Equate both expressions for
`\sigma`

`0.30\mu = (\mu - 88)/(0.4 )`

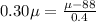
Cross multiply

`0.4*0.30\mu = \mu - 88`

`0.12\mu = \mu - 88`

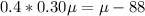
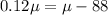
Collect like terms

`0.12\mu - \mu = - 88`

`-0.88\mu = - 88`

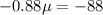
Divide both sides by -0.88

`\mu = 100`

Hence:

`Mean = 100`

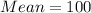
Calculate
`\sigma`

`\sigma = 0.30\mu`

`\sigma = 0.30 * 100`

`\sigma = 30`

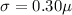
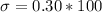
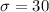
So:

Also, the coefficient of skewness is calculated using:

`Skp = (3 * (Mean - Median))/(\sigma)`

`0.4= (3 * (100 - Median))/(30)`

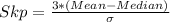
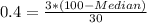
Multiply both sides by 30

`0.4*30= 3 * (100 - Median)`

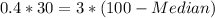
Divide both sides by 3

`0.4*10= 100 - Median`

`4= 100 - Median`

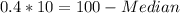
Collect like terms

`Median = 100 - 4`

`Median = 96`