Question

The circumference of the top rim of the cone shaped paper cut is 7.87 inches. Find the least amount of paper that can for a cone shaped cup

Answer 1

14.55 square inches

Explanation:

From the figure it is given that,

The circumference of the top rim of a cone shaped paper cut = 2πr = 7.87 inches

The slant height is l = 3.7 inch

Therefore the least amount of paper which can form a cone shaped cup is the surface area of the cone.

The surface area of the cone is given as :

`$A=(2 \pi r l)/(2)$`

`$A=((2 \pi r) (l))/(2)$`

`$A = ((7.87) * (3.7))/(2)$`

`$A=(29.119)/(2)$`

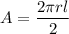
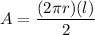
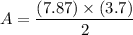
A = 14.55 square inches

Amount of paper required = 14.55 square inches