PART A
Given:
f(x) = 0.69(1.03)x
To find:
If the price of the product is increasing or decreasing and by what percentage
Steps:
we know the formula to find the price of Product A per year, so
f(1) = 0.69 * 1.03 * 1
Price = $0.7107
f(2) = 0.69 * 1.03 * 2
Price = $1.4214
Here the Price of Product after 2 years is greater than the price of Product after one year. So the price of the product A is increasing.
Now to find percentage increase,
Percentage increase =
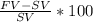 (FV = final value, SV = starting value)
(FV = final value, SV = starting value)
Percentage increase =
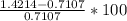
Percentage increase =
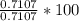
Percentage increase = 100 %
Therefore, the percentage increase of Product A is 100%
PART B
Given:
Price of product B in 1st year = $10,100
Price of product B in 2nd year = $10,201
Price of product B in 3rd year = $10,303.01
Price of product B in 4th year = $10,406.04
To find:
Which product recorded a greater percentage change over the previous year
Steps:
We need to find the percentage change of Product B and Product A of each year. We know that the percentage change of product A is 100 % for each year, so we only need to calculate for product B
PC of product B from 1st to 2nd year =
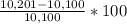
=
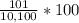
= 0.01 * 100
= 1 %
PC of product B from 2nd to 3rd year =
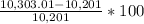
= 1%
PC of product B from 3rd to 4th year
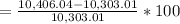
≈ 1%
So, percentage change of product B is 1% per year
Therefore, Product A has greater percentage change
Happy to help :)
If u need more help, feel free to ask