Given:
AD is diameter of the circle, AB is the tangent, and measure of arc ADC is 228 degrees.
To find:
The
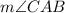 and
and
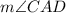 .
.
Solution:
AD is diameter of the circle. So, the measure of arc AD is 180 degrees.
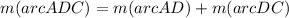
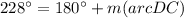

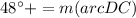
The measure inscribed angle is half of the corresponding subtended arc.
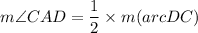
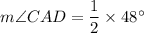
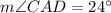
AB is the tangent. So,
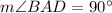 because radius is perpendicular on the tangent and the point of tangency.
because radius is perpendicular on the tangent and the point of tangency.
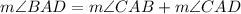



Therefore,
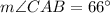 and
and
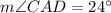 .
.