1 Answer

Plx · Answer 1 · 2022-01-19T02:35:35+0000

Given:

AD is diameter of the circle, AB is the tangent, and measure of arc ADC is 228 degrees.

To find:

The
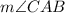$m\angle CAB$ and
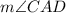$m\angle CAD$ .

Solution:

AD is diameter of the circle. So, the measure of arc AD is 180 degrees.

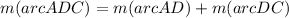
m(arcADC)=m(arcAD)+m(arcDC)

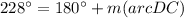
$228^\circ=180^\circ+m(arcDC)$

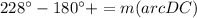
$228^\circ-180^\circ+=m(arcDC)$

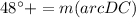
$48^\circ+=m(arcDC)$

The measure inscribed angle is half of the corresponding subtended arc.

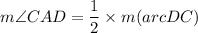
$m\angle CAD=(1)/(2)* m(arcDC)$

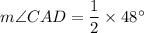
$m\angle CAD=(1)/(2)* 48^\circ$

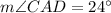
$m\angle CAD=24^\circ$

AB is the tangent. So,
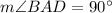$m\angle BAD=90^\circ$ because radius is perpendicular on the tangent and the point of tangency.

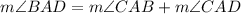
$m\angle BAD=m\angle CAB+m\angle CAD$

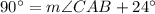
$90^\circ=m\angle CAB+24^\circ$

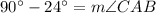
$90^\circ -24^\circ=m\angle CAB$

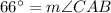
$66^\circ=m\angle CAB$

Therefore,
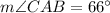$m\angle CAB=66^\circ$ and
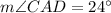$m\angle CAD=24^\circ$ .

Please log in or register to add a comment.