Explanation:
Need to FinD :
- We have to find the angles.
![\red{\frak{Given}} \begin{cases} & \sf {We\ are\ given\ a\ cyclic\ quadrilateral.} \\ & \sf {The\ measures\ of\ the\ opposite\ angles\ of\ the\ quadrilateral\ are\ {\pmb{\sf{(3x\ +\ 10)^(\circ)}}}\ and\ {\pmb{\sf{(2x\ +\ 20)^(\circ)}}}.} \end{cases}]()
We know that,
- The opposite angles of the cyclic quadrilateral are (3x + 10)° and (2x + 20)°. And we have to find the angles.
In a cyclic quadrilateral, all the four vertices of the quadrilateral lie on the circumference of the circle. The opposite angles in a cyclic quadrilateral add up to 180°. So simply, we just simplify the measures and find the value of x. And at last, we'll find the angles of the quadrilateral.

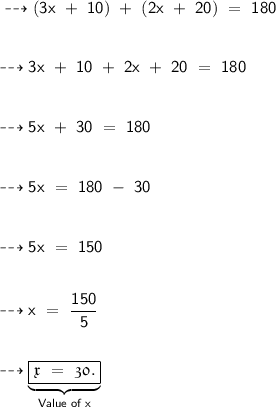
∴ Hence, the required value of x is 30. Now, let us find out the angles.

First AnglE :
- 3x + 10
- 3(30) + 10
- 90 + 10
- 100
∴ Hence, the measure of the first angle of the quadrilateral is 100°.

Second AnglE :
- 2x + 20
- 2(30) + 20
- 60 + 20
- 80
∴ Hence, the measure of the second angle of the quadrilateral is 80°.