Answer:
No real solutions.
Explanation:
We want to solve the equation:
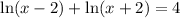
Recall that:
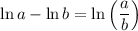
Therefore:
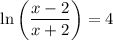
By Definition:
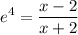
Cross-multiply:

Distribute:

Isolate the x:

Factor:
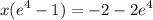
Divide. Therefore:
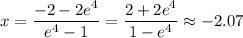
However, note that logs cannot be negative and must be nonzero. According to the first logarithm, x > 2 and according to the second, x > -2. Since the answer is not greater than two, there are no real solutions.