Answer:
∠ CPM = 135°
Explanation:
given AC = BC , then Δ ABC is isosceles with base angles congruent , then
∠ ABC =
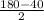 =
=
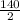 = 70°
= 70°
the exterior angle of a triangle is equal to the sum of the 2 opposite interior angles, then
∠ AMN + ∠ BPM = ∠ ABC , that is
25° + ∠ BPM = 70° ( subtract 25° from both sides )
∠ BPM = 45°
∠ CPM and ∠ BPM are adjacent angles on a straight line and sum to 180°
∠ CPM + 45° = 180° ( subtract 45° from both sides )
∠ CPM = 135°