Answer:
Part A)
A reasonable domain to plot the growth function is:
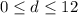
Part B)
The y-intercept represents that when the biologist started her study, the radius of the algae was five millimeters.
Part C)
The average rate of change from d = 4 to d = 11 was about 0.11. This means that from the 4th day to the 11th, the radius of the algae grew, on average, at a rate of 0.11 mm per day.
Explanation:
The radius of the algae f(d) in millimeters after d days is given by the function:
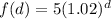
Part A)
We know that the radius of the algae was approximately 6.34 mm when the biologist concluded her study. To find the reasonable domain, we can substitute 6.34 for f(d) and solve for d. Therefore:
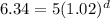
Divide both sides by five:
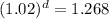
Take the log of both sides with base 1.02:
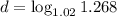
Using the Change of Base Property, evaluate for d:
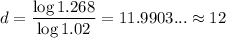
So, the biologist concluded her study after 12 days.
Therefore, a reasonable domain to plot the growth function is:
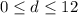
Part 2)
The y-intercept of the function is when d = 0. Find the y-intercept:
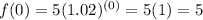
Since d represent the amount of days after the study had begun, the y-intercept represents the radius of the algae on the initial day.
So, when the biologist started her study, the radius of the algae was five millimeters.
Part 3)
To find the average rate of change for a nonlinear function, we find the slope between the two endpoints on the interval.
We want to find the average rate of change of f(d) from d = 4 to d = 11.
Find the endpoints:
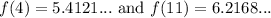
And find the slope between them:
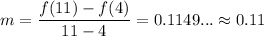
Since f(d) measures millimeters and d measures days, this tells us that, on average, the radius of the algae grew by about 0.11 mm per day from the 4th day to the 11th day.