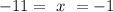Answer:
x = -1 , - 11,
Explanation:
| x | = x
|- x | = x
f(x) = 2 | x + 6 | - 4
x = - 1 , f( - 1) = 2 | - 1 + 6 | - 4 = 2 | 5 | - 4 = 10 - 4 = 6 , True
x = 1 , f( 1 ) = 2 | 1 + 6 | - 4 = 2 | 7 | - 4 = 14 - 4 = 10 , False
x = 11, f( 11 ) = 2 | 11 + 6 | - 4 = 2 | 17 | - 4 = 34 - 4 = 30 , False
x = - 11, f( - 11) = 2 | -11 + 6 | - 4 = 2 | - 5 | - 4 = 10 - 4 = 6 , True
x = 14 , f( 14 ) = 2 | 14 + 6 | - 4 = 2 | 20 | - 4 = 40 - 4 = 36 , False
x = -14 , f( - 14 ) = 2 | - 14 + 6 | - 4 = 2 | - 8 | - 4 = 16 - 4 = 12 , False
x = - 26 , f( - 26) = 2 | -26 + 6 | - 4 = 2 | -20 | - 4 = 40 - 4 = 36 , False
x = 26, f( 26 ) = 2 | 26 + 6 | - 4 = 2 | 32 | - 4 = 64 - 4 = 60 , False
OR
Given f ( x ) = 6
f( x ) = 2 | x + 6 | - 4
6 = 2 | x + 6 | - 4
6 + 4 = 2 | x + 6| - 4 + 4 [ adding 4 to both sides ]
10 = 2 | x + 6 | + 0
5 = | x + 6 | [ dividing both sides by 2 ]
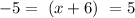
![[ \ | x | = a\ => \ -a \ = x \ = a \ ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/w1wgo0n8dslsdvegl54kprtaa9h27l31ld.png)
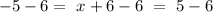
![[ \ subtracting \ by \ 6 \ ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/imj1vrlapbvj0rsahdwtkc9aj09xacyhdd.png)