Answer:
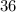
Step-by-step explanation:
The expression
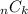 is used to denote the number of ways you can choose
is used to denote the number of ways you can choose
 things from a set of
things from a set of
 things. It is equal to:
things. It is equal to:
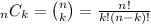
In this case,
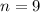 and
and
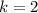 , so:
, so:
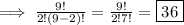
You can also think of it like this:
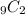 is saying 9 choose 2. We are choosing 2 things from a set of 9 things, where order doesn't matter. For the first thing we choose, there are 9 options. Then 8 options, 7, and so on. Since we're only choosing two things, there are
is saying 9 choose 2. We are choosing 2 things from a set of 9 things, where order doesn't matter. For the first thing we choose, there are 9 options. Then 8 options, 7, and so on. Since we're only choosing two things, there are
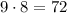 permutations. However, the order of which we choose each thing does not affect what we've chosen overall (e.g. If we're choosing two donut flavors original and strawberry, it doesn't matter which flavor I choose first, because I'm still getting the same two flavors). Therefore, we must divide this by the number of ways we can arrange two distinct values, which is
permutations. However, the order of which we choose each thing does not affect what we've chosen overall (e.g. If we're choosing two donut flavors original and strawberry, it doesn't matter which flavor I choose first, because I'm still getting the same two flavors). Therefore, we must divide this by the number of ways we can arrange two distinct values, which is
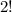 . Our answer is thus
. Our answer is thus
