Answer:
Algebraic "proof" that the solution is 2:
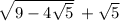
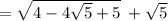
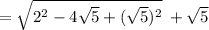
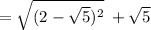
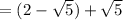
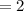
However, this is not the correct mathematical solution to the problem.
The order of operations for
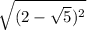 dictate that the operation inside the parentheses must be carried out first.
dictate that the operation inside the parentheses must be carried out first.
As
 , then
, then
 will always be positive.
will always be positive.
If
 is always positive, then
is always positive, then
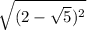 will always be positive.
will always be positive.
As √5 > 2 and
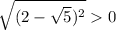 then
then
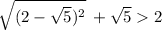
So mathematically, the actual solution to the expression is 2.47 (nearest hundredth) not 2.