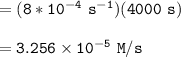Question

The decomposition of hydrogen peroxide was studied, and the following data were obtained at a particular temperature.Time (s) [H2O2] (mol/L)0 1.00120 ± 1 0.91300 ± 1 0.78600 ± 1 0.591200 ± 1 0.371800 ± 1 0.222400 ± 1 0.133000 ± 1 0.0823600 ± 1 0.050 Assuming that the rate= -delta [H2O2]/delta t determine the rate law, integrated rate law, and the value of the rate constant. Calculate [H2O2] at 4000. s after the start of the reaction.

Answer 1

Step-by-step explanation:

From the graphical diagram attached below; we can see the relationship between the concentration of
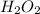`H_2O_2` which declines exponentially in relation to the time and it obeys the equation:
`\mathtt{y = 0.9951 e^{-8* 10^(-4)x}}`

This relates to the 1st order reaction rate, whereby:

The integrated rate law
`\mathtt{ [A] = [A]_o e^(-kt)}`

here:

[A] = reactant concentration at time (t)

[A]_o = initial concentration for the reactant

k = rate constant

As such, the order of the reaction is the first order

Rate constant
`\mathtt{k = 8* 10^(-4) {s^(-1)}}`

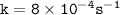
Rate law
`\mathtt{= k[H_2O_2]}`

The integrated rate law
`\mathtt{[H_2O_2] = [H_2O_2]_oe^{-(8*10^(-4))t}}`

From the given table:

the initial concentration of
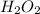`H_2O_2` = 1.00 M

∴

We can determine the concentration of the reactant at 4000s by using the formula:

`\mathtt{[H_2O_2] = [H_2O_2]_oe^{-8*10^(-4)(t)}}`

`\mathtt{[H_2O_2] = (1.00\ M)*e^{-8*10^(-4)(4000)\ s}}`

`\mathtt{[H_2O_2] =0.0407 \ M}`

Finally, at 4000s: the average rate is:

`\mathtt{= (8*10^(-4) \ s^(-1))(4000 \ s) }\\ \\ \mathtt{ = 3.256 * 10^(-5) \ M/s}`