Answer:
See Below.
Explanation:
We want to verify the identity:
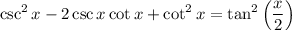
Note that the left-hand side is a perfect square trinomial pattern. Namely:
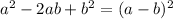
If we let a = csc(x) and b = cot(x), we can factor it as such:
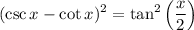
Let csc(x) = 1 / sin(x) and cot(x) = cos(x) / sin(x):
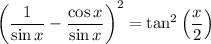
Combine fractions:
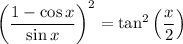
Square (but do not simplify yet):
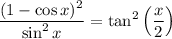
Now, we can make a substitution. Let u = x / 2. So, x = 2u. Substitute:
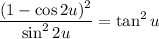
Recall that cos(2u) = 1 - sin²(u). Hence:
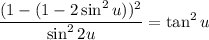
Simplify:
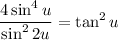
Recall that sin(2u) = 2sin(u)cos(u). Hence:
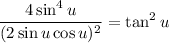
Square:
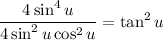
Cancel:
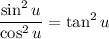
Since sin(u) / cos(u) = tan(u):
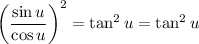
We can substitute u back for x / 2:
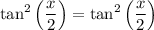
Hence proven.