1 Answer

Kaykun · Answer 1 · 2022-03-28T17:02:23+0000

Given:

In
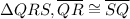$\Delta QRS, \overline{QR}\cong \overline{SQ}$ and
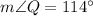$m\angle Q=114^\circ$ .

To find:

The
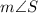$m\angle S$ .

Solution:

In
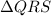$\Delta QRS$ ,

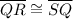
$\overline{QR}\cong \overline{SQ}$

It means the triangle QRS is an isosceles triangle. We know that the base angles of an isosceles triangle are congruent and their measures are equal.

$\angle R\cong \angle S$ [Base angles of isosceles triangle QRS]

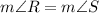$m\angle R=m\angle S$ ...(i)

In
$\Delta QRS$ ,

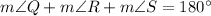
$m\angle Q+m\angle R+m\angle S=180^\circ$

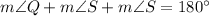$m\angle Q+m\angle S+m\angle S=180^\circ$ [Using (i)]

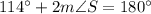
$114^\circ+2m\angle S=180^\circ$

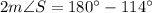
$2m\angle S=180^\circ-114^\circ$

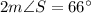
$2m\angle S=66^\circ$

Divide both sides by 2.

$m\angle S=(66^\circ)/(2)$

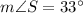
$m\angle S=33^\circ$

Therefore, the
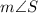$m\angle S$ is 33 degrees.

Please log in or register to add a comment.