Given:
In
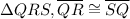 and
and
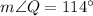 .
.
To find:
The
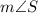 .
.
Solution:
In
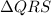 ,
,
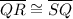
It means the triangle QRS is an isosceles triangle. We know that the base angles of an isosceles triangle are congruent and their measures are equal.
 [Base angles of isosceles triangle QRS]
[Base angles of isosceles triangle QRS]
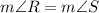 ...(i)
...(i)
In
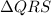 ,
,
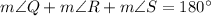
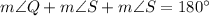 [Using (i)]
[Using (i)]
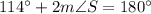
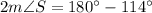
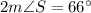
Divide both sides by 2.
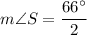
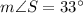
Therefore, the
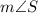 is 33 degrees.
is 33 degrees.