Question

A ball is launched straight up in the air from a height of 6 feet. Its velocity​ (feet/second) t seconds after launch is given by f(t)= -34t+291.

Between 1 second and 8 seconds, the​ ball's height changed by ... feet.
​(Round answer to the nearest​ tenth.)

Answer 1

966 feet

Explanation:

First, we can see that we have the velocity function given, a base value for the height, and need to figure out the change in height. We also know that velocity is the derivative of position/height. Thus, we can find the integral of the velocity to find an equation for the height.

`\int\limits^1_0 {-34t+291} \, dt\\`

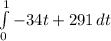
Use the exponent rule to turn -34t into -17t² and 291 into 291t to get our result as

-17t²+291t + C = height (h)

When t=0, we know that our height (h) is 6, so C = 6, making our equation

-17t²+291t + 6

To find the change between 1 second and 8 seconds, we can plug 1 and 8 in for t, and find the difference between those values, which is

(-17(8)²+291(8) + 6) - ( -17(1)²+291(1) + 6 )

= 1246 - 280

= 966

Note that we did final value (t = 8) - initial value (t=1), not the other way around

The change in height, between 1 second and 8 seconds, is therefore 966 feet