Question

Universal Studios is looking to expand in Ontario. The new theme park will be located equidistant to

Newmarket, N (2,8), Markham, M (7,3) and Vaughan, V (-2, 0). Determine the location of the new
theme park if it is located at the point of intersection of the perpendicular bisectors.

Answer 1

Answer: (2, 3)

===============================================

Step-by-step explanation:

For now, we're only going to consider Newmarket and Markham, which are points N and M respectively.

Let's find the slope of line NM through use of the slope formula.

m = (y2-y1)/(x2-x1)

m = (3-8)/(7-2)

m = -5/5

m = -1

Line NM has a slope of -1. Its perpendicular slope is +1 or just 1.

Rule: If the slopes multiply to -1, then the lines are perpendicular.

Or you can apply the negative reciprocal rule to go from -1 to 1.

We'll keep this perpendicular slope in mind for later.

----------------

Now let's find the midpoint of points N and M.

Add up the x coordinates and divide by 2: (x1+x2)/2 = (2+7)/2 = 4.5

Do the same for the y coordinates: (y1+y2)/2 = (8+3)/2 = 5.5

The midpoint of N and M is at (4.5, 5.5)

The perpendicular line must go through these two points. I'm going to skip a few steps here, but basically we go from y = mx+b to y = x+1 after plugging in those x,y values and the perpendicular m we found earlier.

--------------------

In short, the perpendicular bisector for line segment NM is the equation y = x+1.

If you follow the same steps as the previous two sections, but you apply them for points M and V instead, then you should find that the perpendicular bisector is y = -3x+9. I'm skipping steps here as well.

----------------------

At this point, we have the system of equations

`\begin{cases}y = x+1\\y = -3x+9\end{cases}`

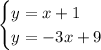
Let's use substitution to solve for x and y

y = x+1

-3x+9 = x+1

-3x-x = 1-9

-4x = -8

x = -8/(-4)

x = 2

y = x+1

y = 2+1

y = 3

So together, x = 2 and y = 3 pair up to get the ordered pair solution (x,y) = (2,3)

This is the location where the theme park should be placed. Let's say that C = (2,3). I'm using C for center.

You can use the distance formula to confirm that segments CN, CM and CV are all the same length, which would verify that point C is equidistant from all the other points. Furthermore, it means that points N, M and V are all on the same circle centered at C.

I know it says not to use a graph, but it still helps to see what's going on. Also, it's a handy way to confirm the answer. I used GeoGebra to make the graph. See the diagram below.

Side note: you only need 2 perpendicular bisectors to find point C. You could use three, but that's overkill since they all intersect at the same location.