Answer:
Left 2 units
Explanation:
Without knowing what f(x), it is impossible to answer this question. I'll answer assuming a parent function of
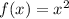 .
.
In the function
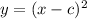 ,
,
 represents the phase shift from parent function
represents the phase shift from parent function
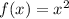 . If
. If
 is positive (e.g.
is positive (e.g.
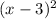 ), then the function shifts to the right however many units
), then the function shifts to the right however many units
 is. If
is. If
 is negative (e.g.
is negative (e.g.
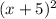 ), the function shifts to the left however many units the absolute value of
), the function shifts to the left however many units the absolute value of
 is.
is.
In the function
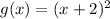 , let's find out the value of
, let's find out the value of
 :
:
Format:
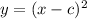
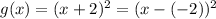
Therefore,
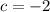 .
.
Since
 is negative, the function must shift to the left. To find out how many units it shifts to the left, take the absolute value of
is negative, the function must shift to the left. To find out how many units it shifts to the left, take the absolute value of
 :
:
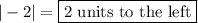 .
.
Thus, the graph of
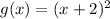 is a translation of the graph
is a translation of the graph
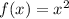 by 2 units to the left.
by 2 units to the left.
*Note: Once again, this answer is assuming
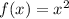 as it is not clarified in the question. If
as it is not clarified in the question. If
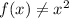 and is already shifted, you will need to account for shift. If you believe this is the case, feel free to let me know in the comments.
and is already shifted, you will need to account for shift. If you believe this is the case, feel free to let me know in the comments.