Question

Health insurance benefits vary by the size of the company (the Henry J. Kaiser Family Foundation website, June 23, 2016). The sample data below show the number of companies providing health insurance for small, medium, and large companies. For the purposes of this study, small companies are companies that have fewer than employees. Medium-sized companies have to employees, and large companies have or more employees. The questionnaire sent to employees asked whether or not the employee had health insurance and then asked the enployee to indicate the size of the company. Health Insurance Size of Company Yes No Total Small 33 17 50 Medium 68 7 75 Large 88 12 100 a. Conduct a test of independence to determine whether health insurance coverage is independent of the size of the company. What is the -value? Compute the value of the test statistic (to 2 decimals). The -value is - Select your answer - Using level of significance, what is your conclusion? - Select your answer - b. A newspaper article indicated employees of small companies are more likely to lack health insurance coverage. Calculate the percentages of employees without health insurance based on company size (to the nearest whole number). Small Medium Large Based on the percentages calculated above, what can you conclude? - Select your answer -

Answer 1

There is not enough statistical evidence to suggest that the health insurance coverage is independent of the size of the company

Explanation:

The given data presented in tabular form is presented as follows;

`\begin{array}{llcr}&Health \ Insurance&\\Size \ of \ Company & Yes &No &Total\\Small&34&16&50\\Medium&61&14&75\\Large&85&15&100\end{array}`

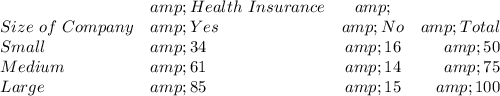
The null hypothesis, H₀; The two data are independent

The alternative hypothesis Hₐ; The variables are dependent

`Expected \ value = ((Row \ total) * (Column \ total) )/(Table \ total)`

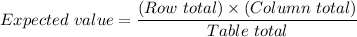
The expected value are the values in parenthesis in the following table;

`\begin{array}{llcr}&Health \ Insurance&\\Size \ of \ Company & Yes &No &Total\\Small&34(40)&16(10)&50\\Medium&61(60)&14(15)&75\\Large&85(80)&15(20)&100\\Total&180&45&225\end{array}`

`\chi ^2 = \sum{( \left(O_i - E_i \right)^2)/(E_i)`

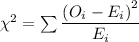
Therefore

χ² = (34 - 40)²/40 + (16 - 10)²/10 + (61 - 60)²/60 + (14 - 15)²/15 + (85 - 80)²/80 + (15 - 20)²/20 ≈ 6.1458

The degrees of freedom = (2 - 1)·(3 - 1) = 2

The p-value from the Chi-square table is 0.05 < p-value < 0.01

Given that the p-value is larger than the significant value, we have that data is not statistically significant and we fail to reject the null hypothesis.

Therefore, the health insurance coverage is independent of the size of the company