Question

A rectangular metal tank with an open top is to hold cubic feet of liquid. What are the dimensions of the tank that require the least material to%E2%80%8B build?

Answer 1

`h = 3.5`

`w = 7`

`l = 7`

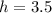
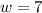
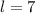
Explanation:

Given

`Volume = 171.5ft^3`

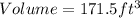
Required

The dimension that requires least material

The volume is:

`Volume = lwh`

Where:

`l \to length`

`w \to width`

`h \to height`

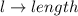
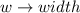
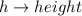
So, we have:

`171.5 = lwh`

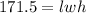
Make l the subject

`l = (171.5)/(wh)`

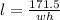
The surface area (A) of an open-top rectangular tank is:

`A = lw + 2lh + 2wh`

Substitute:
`l = (171.5)/(wh)`

`A = (171.5)/(wh) * w + 2*(171.5)/(wh)*h + 2wh`

`A = (171.5)/(h) + 2*(171.5)/(w) + 2wh`

`A = (171.5)/(h) + (343)/(w) + 2wh`

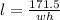
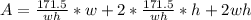
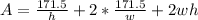
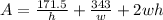
Rewrite as:

`A = 171.5h^(-1) + 343w^(-1) + 2wh`

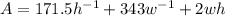
Differentiate with respect to h and w

`A_h = -171.5h^(-2) +2w`

`A_w = -343w^(-2) +2h`

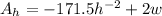
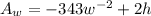
Equate both to 0

`-171.5h^(-2) +2w=0`

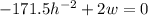
Make w the subject

`2w = 171.5h^(-2)`

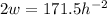
Divide by 2

`w = 85.75h^(-2)`

`-343w^(-2) +2h = 0`

Make h the subject

`2h = 343w^(-2)`

Divide by 2

`h = 171.5w^(-2)`

`h = (171.5)/(w^2)`

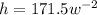
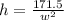
Substitute
`w = 85.75h^(-2)` in
`h = (171.5)/(w^2)`

`h = (171.5)/((85.75h^(-2))^2)`

`h = (171.5)/(85.75^2*h^(-4))`

`h = (2)/(85.75*h^(-4))`

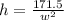
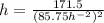
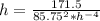
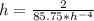
Multiply both sides by
`h^(-4)`

`h^(-4) * h = (1)/(85.75*h^(-4)) * h^(-4)`

`h^(-3) = (2)/(85.75)`

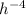
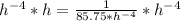
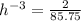
Rewrite as:

`(1)/(h^3) = (2)/(85.75)`

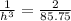
Inverse both sides

`h^3 = 85.75/2`

`h^3 = 42.875`

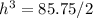
Take cube roots

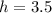`h = 3.5` ---- height

Recall that:
`w = 85.75h^(-2)`

`w = 85.75 * 3.5^(-2)`

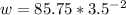
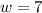`w = 7` --- width

Recall that:
`l = (171.5)/(wh)`

`l = (171.5)/(3.5 * 7)`

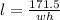
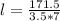
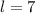`l = 7` --- length