Question

R = sec(θ) − 2cos(θ), where -π/2 < θ < π/2

Convert this equation to rectangular coordinates.

Answer 1

y = (x/(1-x))√(1-x²)

Explanation:

The equation can be translated to rectangular coordinates by using the relationships between polar and rectangular coordinates:

x = r·cos(θ)

y = r·sin(θ)

x² +y² = r²

__

r = sec(θ) -2cos(θ)

r·cos(θ) = 1 -2cos(θ)² . . . . . . . . multiply by cos(θ)

r²·r·cos(θ) = r² -2r²·cos(θ)² . . . multiply by r²

(x² +y²)x = x² +y² -2x² . . . . . . . substitute rectangular relations

x²(x +1) = y²(1 -x) . . . . . . . . . . . subtract xy²-x², factor

y² = x²(1 +x)/(1 -x) = x²(1 -x²)/(1 -x)² . . . . multiply by (1-x)/(1-x)

`\boxed{y=(x√(1-x^2))/(1-x)}`

__

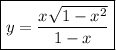
The attached graph shows the equivalence of the polar and rectangular forms.