Question

The tub of a washer goes into its spin-dry cycle, starting from rest and reaching an angular speed of 3.0 rev/s in 13.0 s. At this point, the person doing the laundry opens the lid, and a safety switch turns off the washer. The tub slows to rest in 12.0 s. Through how many revolutions does the tub turn during this 25 s interval

Answer 1

The tub turns 37.520 revolutions during the 25-second interval.

Step-by-step explanation:

The total number of revolutions done by the tub of the washer (
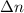`\Delta n`), in revolutions, is the sum of the number of revolutions done in the acceleration (
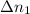`\Delta n_(1)`), in revolutions, and deceleration stages (
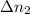`\Delta n_(2)`), in revolutions:

`\Delta n = \Delta n_(1) + \Delta n_(2)` (1)

Then, we expand the previous expression by kinematic equations for uniform accelerated motion:

`\Delta n = (1)/(2)\cdot ( \ddot n_(1)\cdot t_(1)^(2) - \ddot n_(2) \cdot t_(2)^(2))` (1b)

Where:

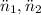`\ddot n_(1), \ddot n_(2)` - Angular accelerations for acceleration and deceleration stages, in revolutions per square second.

`t_(1), t_(2)` - Acceleration and deceleration times, in seconds.

And each acceleration is determined by the following formulas:

Acceleration

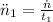`\ddot n_(1) = (\dot n)/(t_(1))` (2)

Deceleration

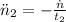`\ddot n_(2) = -(\dot n)/(t_(2) )` (3)

Where
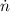`\dot n` is the maximum angular velocity of the tub of the washer, in revolutions per second.

If we know that
`\dot n = 3\,(rev)/(s)`,
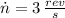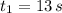`t_(1) = 13\,s` and
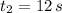`t_(2) = 12\,s`, then the quantity of revolutions done by the tub is:

`\ddot n_(1) = (3\,(rev)/(s) )/(13\,s)`

`\ddot n_(1) = 0.231\,(rev)/(s^(2))`

`\ddot n_(2) = -(3\,(rev)/(s) )/(12\,s)`

`\ddot n_(2) = -0.25\,(rev)/(s^(2))`

`\Delta n = (1)/(2)\cdot ( \ddot n_(1)\cdot t_(1)^(2) + \ddot n_(2) \cdot t_(2)^(2))`

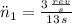
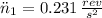
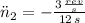
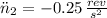
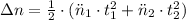
`\Delta n = (1)/(2)\cdot \left[\left(0.231\,(rev)/(s^(2)) \right)\cdot (13\,s)^(2)-\left(-0.25\,(rev)/(s^(2)) \right)\cdot (12\,s)^(2)\right]`

`\Delta n = 37.520\,rev`

The tub turns 37.520 revolutions during the 25-second interval.