Answer:
The tub turns 37.520 revolutions during the 25-second interval.
Step-by-step explanation:
The total number of revolutions done by the tub of the washer (
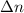 ), in revolutions, is the sum of the number of revolutions done in the acceleration (
), in revolutions, is the sum of the number of revolutions done in the acceleration (
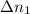 ), in revolutions, and deceleration stages (
), in revolutions, and deceleration stages (
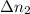 ), in revolutions:
), in revolutions:
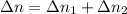 (1)
(1)
Then, we expand the previous expression by kinematic equations for uniform accelerated motion:
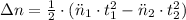 (1b)
(1b)
Where:
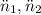 - Angular accelerations for acceleration and deceleration stages, in revolutions per square second.
- Angular accelerations for acceleration and deceleration stages, in revolutions per square second.
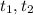 - Acceleration and deceleration times, in seconds.
- Acceleration and deceleration times, in seconds.
And each acceleration is determined by the following formulas:
Acceleration
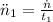 (2)
(2)
Deceleration
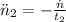 (3)
(3)
Where
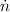 is the maximum angular velocity of the tub of the washer, in revolutions per second.
is the maximum angular velocity of the tub of the washer, in revolutions per second.
If we know that
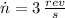 ,
,
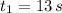 and
and
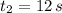 , then the quantity of revolutions done by the tub is:
, then the quantity of revolutions done by the tub is:
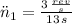
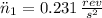
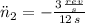
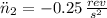
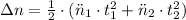
![\Delta n = (1)/(2)\cdot \left[\left(0.231\,(rev)/(s^(2)) \right)\cdot (13\,s)^(2)-\left(-0.25\,(rev)/(s^(2)) \right)\cdot (12\,s)^(2)\right]](https://img.qammunity.org/2022/formulas/physics/college/gyziq7adpg47y31rgns5ux66fgd2nrwf9q.png)
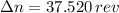
The tub turns 37.520 revolutions during the 25-second interval.