Answer: The value of x is 5.970.
Explanation:
Given: The square has sides length of X cm.
Let r be the radius of the circle.
The square fits exactly inside a circle with each of the vertices being on the circumference of the circle.
Then diagonal of square = diameter of circle
i.e.
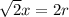 [Diagonal of square =
[Diagonal of square =
 (side)]
(side)]
i.e.
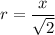
area of circle =
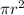
i.e.
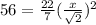
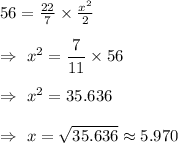
Hence, the value of x is 5.970.