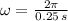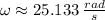Question

Una prenda de 320gramos de ropa gira en el interior de una lavadora si dicha lavadora tiene 40 cm y gira con una frecuencia de 4 hz halla el periodo la velocidad angular la fuerza con la que gira la prenda y la velocidad lineal de la lavadora

Answer 1

Período del tambor:
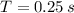`T = 0.25\,s`, fuerza sobre la prenda:
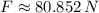`F \approx 80.852\,N`, velocidad lineal del tambor:
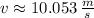`v \approx 10.053\,(m)/(s)`, velocidad angular del tambor:
`\omega \approx 25.133\,(rad)/(s)`.

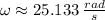Step-by-step explanation:

La expresión tiene un error por omisión, su forma correcta queda descrita a continuación:

"Una prenda de 320 gramos de ropa gira en el interior de una lavadora si dicha lavadora tiene un radio de 40 centímetros y gira con una frecuencia de 4 hertz. Halle a) el período, b) la velocidad angular, c) la fuerza con la que gira la prenda y d) la velocidad lineal de la lavadora."

El tambor gira a velocidad angular constante (
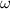`\omega`), en radianes por segundo, lo cual significa que la prenda experimenta una aceleración centrífuga (
`a`), en metros por segundo al cuadrado. En primer lugar, calculamos el período de rotación del tambor (
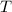`T`), en segundos:

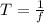`T = (1)/(f)` (1)

Donde
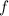`f` es la frecuencia, en hertz.

(
`f = 4\,hz`)

`T = (1)/(4\,hz)`

`T = 0.25\,s`

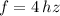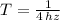
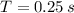
Ahora determinamos la fuerza aplicada sobre la prenda (
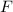`F`), en newtons:

`F = m\cdot a` (2)

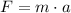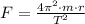`F = (4\pi^(2)\cdot m \cdot r)/(T^(2))` (2b)

Donde:

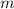`m` - Masa de la prenda, en kilogramos.

`r` - Radio interior del tambor, en metros.

(
`m = 0.32\,kg`,
`r = 0.4\,m`,
`T = 0.25\,s`)

`F = (4\pi^(2)\cdot (0.32\,kg)\cdot (0.4\,m))/((0.25\,s)^(2))`

`F \approx 80.852\,N`

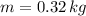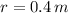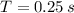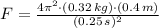
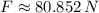
La velocidad lineal de la lavadora es:

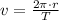`v = (2\pi\cdot r)/(T)` (3)

(
`r = 0.4\,m`,
`T = 0.25\,s`)

`v = (2\pi\cdot (0.4\,m))/(0.25\,s)`

`v \approx 10.053\,(m)/(s)`

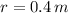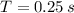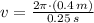
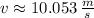
Y la velocidad angular del tambor de la lavadora:

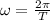
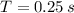`\omega = (2\pi)/(T)`

(
`T = 0.25\,s`)

`\omega = (2\pi)/(0.25\,s)`

`\omega \approx 25.133\,(rad)/(s)`