Question

12.) The FAA has to periodically revise their rules regarding weight estimates that vary by

season. Airlines currently use an estimate for the weight of an adult male passenger of 190 lbs.
in the summer that assumes
he carries sixteen pounds of baggage and has five pounds of
clothing. According to your textbook, assume that men (not clothed nor carrying baggage) have
weights that are normally distributed with a mean of 188.6 lbs. and a standard deviation of 38.9
lbs.

a.) If one adult male is randomly selected and is assumed to be also carrying 21 lbs. due to
clothing and baggage, find the probability that the total weight is greater than 190 lbs.

b.) What total weight would separate the lower 20% of men carrying 21 lbs. of clothing and
baggage from the top 80%?

Answer 1

a) 0.4856 = 48.56% probability that the total weight is greater than 190 lbs.

b) A total weight of 155.9 lbs.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Mean of 188.6 lbs. and a standard deviation of 38.9 lbs.

This means that

`Z = (190 - 188.6)/(38.9)`

`Z = 0.036`

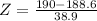
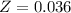
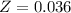`Z = 0.036` has a p-value of 0.5144.

1 - 0.5144 = 0.4856.

0.4856 = 48.56% probability that the total weight is greater than 190 lbs.

b.) What total weight would separate the lower 20% of men carrying 21 lbs. of clothing and baggage from the top 80%?

This is the 20th percentile, which is X when Z has a p-value of 0.2, so X when Z = -0.84.

`Z = (X - \mu)/(\sigma)`

`-0.84 = (X - 188.6)/(38.9)`

`X - 188.6 = -0.84*38.9`

`X = 155.9`

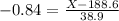
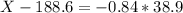
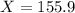
A total weight of 155.9 lbs.