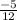Question
Determine tan(t) if cos(t) = -12/13 and sin(t) = 5/13
Answer:
tan(t) =
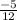
Explanation:
Method 1:
The sketch of the trigonometry is attached to this response.
Since cos(t) is negative and sin(t) is positive, then t should be in the second quadrant as shown in the sketch. A triangle is formed.
We know that, in a given triangle, the cosine of a given angle is the ratio of the adjacent side to the hypotenuse side.
i.e
cos (t) = adjacent / hypotenuse = - 12 / 13
Where;
adjacent = -12 [the adjacent side is in the -x direction]
hypotenuse = 13
Also, the sine of a given angle is the ratio of the opposite side to the hypotenuse side.
sin (t) = opposite / hypotenuse
Where;
opposite = 5
hypotenuse = 13
These sides - opposite, adjacent and hypotenuse - are labelled in the sketch.
From this triangle and the labels, the tangent can be found.
We know that the tangent of a given angle is the ratio of the opposite side to the hypotenuse side. i.e
tan (t) = opposite / adjacent
Where;
opposite = 5
adjacent = -12
Therefore,
tan (t) =
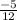
Method 2:
The tangent of an angle is the ratio of the sine of that angle to the cosine of that angle. i.e
tan(t) = sin(t) / cos (t) ---------------(i)
sin(t) = 5 / 13
cos(t) = -12 / 13
Substitute for sin(t) and cos (t) in equation (i)
tan(t) = [5 / 13] / [-12 / 13]
tan(t) = [5 / 13] x [-13 / 12]
tan(t) =
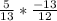
tan(t) =