Question

A whole number is 6 more than 2 times another number. The sum of the two numbers is less than 50. This can be written in an inequality as x+2x+6<50, where xrepresents the smaller number.

From the set (13, 14, 15, 16, 17), the values of x for which the inequality holds true are

Answer 1

13, 14

Explanation:

The parameters of the numbers are;

A whole number value = 2 × Another number + 6

The sum of the two numbers is less than 50

Given that the first number is equal to more than twice the second number, we have that the first number is the larger number, while the second number is the smaller number

Where 'x' represents the second number, we get;

x + 2·x + 6 < 50

Simplifying gives;

3·x + 6 < 50

x < (50 - 6)/3 = 14.
`\overline 6`

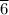
x < 14.
`\overline 6`

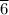
Therefore, the numbers for which the inequality holds true are numbers less than 14.
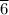`\overline 6`. From the given option, the numbers are 13, and 14.