Question

The hypotenuse of a right triangle is 13 ft long. The longer leg is 7 ft longer than the shorter leg. Find the side lengths of the triangle.

Answer 1

The shorter leg is five feet, the longer leg is 12 feet, and the hypotenuse is 13 feet.

Explanation:

Let the shorter leg be x.

Since the longer leg is seven feet longer than the shorter leg, the length of the longer leg can be modeled by (x + 7).

Since the triangle is a right triangle, we can use the Pythagorean Theorem, given by:

`a^2+b^2=c^2`

Where a and b are the side lengths and c is the hypotenuse.

The hypotenuse is 13 and the legs are x and (x + 7). Substitute:

`(x)^2+(x+7)^2=(13)^2`

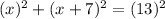
Square:

`x^2+x^2+14x+49=169`

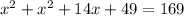
Simplify:

`2x^2+14x-120=0`

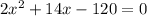
We can divide both sides by two:

`x^2+7x-60=0`

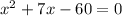
Factor:

`(x-5)(x+12)=0`

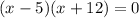
Zero Product Property:

`x-5=0\text{ or }x+12=0`

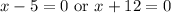
Solve for each case:

`x=5\text{ or } x=-12`

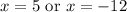
Since lengths cannot be negative, we can ignore the negative answer. So, our only solution is:

`x=5`

The shorter leg is five feet, the longer leg will be (5 + 7) or 12 feet. And the hypotenuse is 13 feet as given.