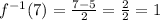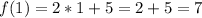Question

If f (x) = 2 x + 5 and three-halves are inverse functions of each other and f (x) = 2x + 5, what is

Answer 1

See explanation

Explanation:

The question has conflicting details

`f(x) = 2x + 5`

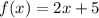
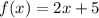`f(x) = 2x + 5` and three halves doesn't sound correct.

So, I will take f(x) as

`f(x) = 2x + 5`

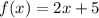
Next, solve for the inverse function

Replace f(x) with y

`y = 2x + 5`

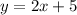
Swap x and y

`x = 2y + 5`

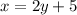
Make 2y the subject

`2y = x-5`

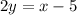
Make y the subject

`y = (x-5)/(2)`

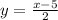
Replace y with the inverse sign

`f^(-1)(x) = (x-5)/(2)`

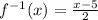
So, now we can calculate any value from the original function and from the inverse function.

For instance:

`f^(-1)(7) = (7-5)/(2) = (2)/(2) = 1`

`f(1) = 2*1 + 5 = 2+5=7`